【CodeForces 538F】A Heap of Heaps / 题解

原题地址

题目描述

给定一个长度为$n$的数列，对于 $1~n-1$ 的所有 $k$，建造一个完全$k$叉数。对于每一个$k$，求父亲比儿子大的节点对数。

样例

输入

5
1 5 4 3 2

输出

3 2 1 0

样例解释

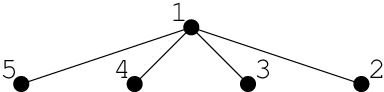
思路

我们很容易发现，对于一个点，一定范围的k内它的父亲节点位置是相同的。因为题目给了点$i$父亲的定义是$(i-2)/k+1$，你会发现取值的种类是$sqrt(n)$级别的。。。
所以我们直接枚举对于每个节点的不同的父亲，用差分数组维护区间加，最后求前缀和得到答案。

代码

#include 
#define ll long long
#define maxn 200100
using namespace std;
ll a[maxn],sum[maxn],n;
int main(){
    ios::sync_with_stdio(false);
    cin>>n;
    for (int i=1;i<=n;i++) cin>>a[i];
    for (int i=2;i<=n;i++){
        int v=i-2,t;
        for (int j=1;j<=v;j=t+1){
            t=v/(v/j);
            if (a[v/j+1]>a[i]) sum[j]++,sum[t+1]--;
        }
        if (a[1]>a[i]) sum[i-1]++,sum[n]--;
    }
    for (int i=1;i