比赛地址
A. Photo of The Sky
Statement
There is a beautiful garden of stones in Innopolis.
Its most beautiful place is the n piles with stones numbered from $n$.
EJOI participants have visited this place twice.
When they first visited it, the number of stones in piles was $x_1, x_2, ldots, x_n$, correspondingly. One of the participants wrote down this sequence in a notebook.
They visited it again the following day, and the number of stones in piles was equal to $y_1, y_2, ldots, y_n$. One of the participants also wrote it down in a notebook.
It is well known that every member of the EJOI jury during the night either sits in the room $108$ or comes to the place with stones. Each jury member who comes there either takes one stone for himself or moves one stone from one pile to another. We can assume that there is an unlimited number of jury members. No one except the jury goes to the place with stones at night.
Participants want to know whether their notes can be correct or they are sure to have made a mistake.
I/O
Input
The first line of the input file contains a single integer $n$, the number of piles with stones in the garden $1 leq n leq 50$.
The second line contains n integers separated by spaces $x_1, x_2, ldots, x_n$, the number of stones in piles recorded in the notebook when the participants came to the place with stones for the first time ($0 leq x_i leq 1000$).
The third line contains $n$ integers separated by spaces $y_1, y_2, ldots, y_n$, the number of stones in piles recorded in the notebook when the participants came to the place with stones for the second time ($0 leq y_i leq 1000$).
Output
If the records can be consistent output “Yes”, otherwise output “No” (quotes for clarity).
Sample
Input
5
1 1 1 1 1
1 0 1 0 1Output
YesIdea
首先我们对给定的序列排个序。
我们要使矩形面积尽量小,那么我们不妨从序列中选取连续的 $n$ 个数作为不同点的横坐标。可以证明(我才不证明给你看呢)这是科学的,因为通过交换数字使序列不连续不会使答案变优。
所以我们可以 $O(n)$ 枚举选出的连续横坐标序列的最小值,$O(1)$ 计算对于每一个位置的答案。
Code
#include
#define maxn 100010
#define ll long long
#define INF 1e18+5
using namespace std;
int a[maxn<<1],n;
ll ans=INF;
int main(){
ios::sync_with_stdio(false);
cin>>n;
for (int i=1;i<=2*n;i++)
cin>>a[i];
sort(a+1,a+1+2*n);
for (int l=1;l<=n;l++){
ll wid=a[l+n-1]-a[l];
ll het=a[2*n]-a[(l==1?n+1:1)];
ans=min(ans,wid*het);
}
cout< B. Chemical table
Statement
Innopolis University scientists continue to investigate the periodic table. There are n·m known elements and they form a periodic table: a rectangle with n rows and m columns. Each element can be described by its coordinates (r, c) (1 ≤ r ≤ n, 1 ≤ c ≤ m) in the table.
Recently scientists discovered that for every four different elements in this table that form a rectangle with sides parallel to the sides of the table, if they have samples of three of the four elements, they can produce a sample of the fourth element using nuclear fusion. So if we have elements in positions (r1, c1), (r1, c2), (r2, c1), where r1 ≠ r2 and c1 ≠ c2, then we can produce element (r2, c2).
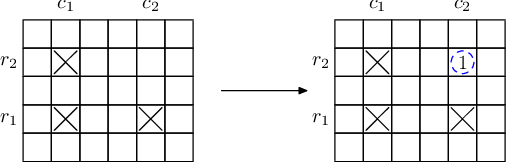
Samples used in fusion are not wasted and can be used again in future fusions. Newly crafted elements also can be used in future fusions.
Innopolis University scientists already have samples of q elements. They want to obtain samples of all n·m elements. To achieve that, they will purchase some samples from other laboratories and then produce all remaining elements using an arbitrary number of nuclear fusions in some order. Help them to find the minimal number of elements they need to purchase.
I/O
Input
The first line contains three integers n, m, q (1 ≤ n, m ≤ 200 000; 0 ≤ q ≤ min(n·m, 200 000)), the chemical table dimensions and the number of elements scientists already have.
The following q lines contain two integers ri, ci (1 ≤ ri ≤ n, 1 ≤ ci ≤ m), each describes an element that scientists already have. All elements in the input are different.
Output
Print the minimal number of elements to be purchased.
Sample
Input
4 3 6
1 2
1 3
2 2
2 3
3 1
3 3Output
1Note
There are several possible solutions. One of them is illustrated below.
Note that after purchasing one element marked as red it's still not possible to immidiately produce the middle element in the bottom row (marked as 4). So we produce the element in the left-top corner first (marked as 1), and then use it in future fusions.
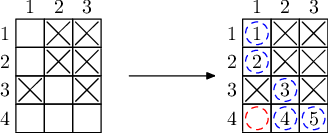
Idea
我们用二分图建图即可。
二分图中节点为行号和列号,对于原图中存在的点,连接二分图中的行号和列号。我们发现每三个满足条件的节点连边后会形成一个联通块。我们要填满原图,就是让原图形成一个联通块,那么需要购买的元素就是联通块数量减一。
Code
// Chemical_table.cpp : Defines the entry point for the console application.
// XG_Zepto, 7/31/2018. All rights reserved.
#include "stdafx.h"
#include
#include
#include
#include
#define maxn 200100
using namespace std;
struct Edge{
int to,next;
Edge(int a=0,int b=0){
to=a,next=b;
}
}l[maxn<<2];
int head[maxn<<1],m,cnt,n,q,ans,vis[maxn<<1];
void Add(int a,int b){
l[++cnt]=Edge(b,head[a]);
head[a]=cnt;
}
void Dfs(int u){
vis[u]=1;
for(int i=head[u];i;i=l[i].next){
if (!vis[l[i].to]) Dfs(l[i].to);
}
}
int main(){
ios::sync_with_stdio(false);
cin>>n>>m>>q;
for(int i=1;i<=q;i++){
int x,y;
cin>>x>>y;
Add(x,y+n);
Add(y+n,x);
}
for (int i=1;i<=n+m;i++)
if (!vis[i]) Dfs(i),ans++;
cout< C. Hills
Statement
Welcome to Innopolis city. Throughout the whole year, Innopolis citizens suffer from everlasting city construction.
From the window in your room, you see the sequence of n hills, where i-th of them has height ai. The Innopolis administration wants to build some houses on the hills. However, for the sake of city appearance, a house can be only built on the hill, which is strictly higher than neighbouring hills (if they are present). For example, if the sequence of heights is 5, 4, 6, 2, then houses could be built on hills with heights 5 and 6 only.
The Innopolis administration has an excavator, that can decrease the height of an arbitrary hill by one in one hour. The excavator can only work on one hill at a time. It is allowed to decrease hills up to zero height, or even to negative values. Increasing height of any hill is impossible. The city administration wants to build k houses, so there must be at least k hills that satisfy the condition above. What is the minimum time required to adjust the hills to achieve the administration's plan?
However, the exact value of k is not yet determined, so could you please calculate answers for all k in range 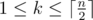 ? Here
? Here  denotes n divided by two, rounded up.
denotes n divided by two, rounded up.
I/O
Input
The first line of input contains the only integer n (1 ≤ n ≤ 5000)—the number of the hills in the sequence.
Second line contains n integers ai (1 ≤ ai ≤ 100 000)—the heights of the hills in the sequence.
Output
Print exactly  numbers separated by spaces. The i-th printed number should be equal to the minimum number of hours required to level hills so it becomes possible to build i houses.
numbers separated by spaces. The i-th printed number should be equal to the minimum number of hours required to level hills so it becomes possible to build i houses.
Sample
Input
5
1 1 1 1 1Output
1 2 2 Note
In the first example, to get at least one hill suitable for construction, one can decrease the second hill by one in one hour, then the sequence of heights becomes 1, 0, 1, 1, 1 and the first hill becomes suitable for construction.
In the first example, to get at least two or at least three suitable hills, one can decrease the second and the fourth hills, then the sequence of heights becomes 1, 0, 1, 0, 1, and hills 1, 3, 5 become suitable for construction.
Idea
首先,我们可以预处理出对于每个 hill,要使得它满足条件需要在左边和右边分别付出的代价 $l_i,r_i$。
然后我们可以 $O(n^2)$ DP。设 $f[i][j][k]$ 为考虑前 $i$ 个 hill,$j$ 个 hill 满足条件,第 $i$ 个 hill 的使用情况为 $k$。 显然 $k$ 只有 0 或 1 两种可能。
然后考虑转移方程。对于 $f[i][j][0]$,它可以直接由左边的 hill 的状态转移过来,因为在计算上个状态的时候,已经考虑了 $i$ 对它的影响。显然,有 $f[i][j][0]=min(f[i-1][j][0],f[i-1][j][1])$。
对于 $f[i][j][1]$,我们知道左边的 hill 一定没有使用,可以直接由 $f[i-1][j-1][0]+l[i]+r[i]$ 转移过来。
如果你只写了这个,你就 Gay Gay 了。为什么呢?
我们知道 $f[i-1][j-1][0]=min(f[i-2][j-1][0],f[i-2][j-1][1])$,而 $f[i-2][j-1][1]$ 之中可能已经考虑了 $i-1$ 的高度的影响。这个时候你再无脑加上 $l[i]$ 就可能影响答案。
解决方案是再考虑一下这个值:$f[i-2][j-1][1]+max(0,a[i-2]-a[i])+r[i]$。这样可以规避可能的重复计算,保证答案的正确性。
Code
#include
#define inf 0x3f3f3f3f
#define maxn 5001
using namespace std;
int n,f[maxn][maxn][2],l[maxn],r[maxn],a[maxn];
int main(){
ios::sync_with_stdio(false);
cin>>n;
int un=n/2+(n&1);
memset(f,inf,sizeof(f));
for (int i=1;i<=n;i++) cin>>a[i];
for (int i=1;i<=n;i++){
l[i]=max(0,a[i-1]-a[i]+1);
r[i]=max(0,a[i+1]-a[i]+1);
}
f[0][0][0]=0;
for (int i=1;i<=n;i++){
f[i][0][0]=0;
for (int j=1;j<=(i+1)/2;j++){
f[i][j][0]=min(f[i-1][j][0],f[i-1][j][1]);
f[i][j][1]=min(f[i-1][j-1][0]+l[i]+r[i],i>2?f[i-2][j-1][1]+max(0,a[i-2]-a[i])+r[i]:inf);
}
}
for (int i=1;i<=un;i++)
cout< D. AB-Strings
Statement
Your task is to find a sequence of operations after which one of the strings consists only of a letters and the other consists only of b letters. The number of operations should be minimized.
I/O
Input
The first line contains a string $s$ ($1 ≤ |s| ≤ 2·10^5$).
The second line contains a string $t$ ($1 ≤ |t| ≤ 2·10^5$).
Here $|s|$ and $|t|$ denote the lengths of $s$and $t$, respectively. It is guaranteed that at least one of the strings contains at least one $a$ letter and at least one of the strings contains at least one $b$ letter.
Output
The first line should contain a single integer $n$ ($0 ≤ n ≤ 5·10^5$) — the number of operations.
Each of the next $n$ lines should contain two space-separated integers $a_i$, $b_i$ — the lengths of prefixes of $s$ and $t$ to swap, respectively.
If there are multiple possible solutions, you can print any of them. It's guaranteed that a solution with given constraints exists.
Sample
Input
bab
bb
Output
2
1 0
1 3
Note
In the first example, you can solve the problem in two operations:
- Swap the prefix of the first string with length 1 and the prefix of the second string with length 0. After this swap, you'll have strings ab and bbb.
- Swap the prefix of the first string with length 1 and the prefix of the second string with length 3. After this swap, you'll have strings bbbb and a.
